3.1.0: A Walk Through the View Part 1
Movement in three dimensions is not a quick and easy topic. There are many difficult concepts involved and a lot of math. To help us encapsulate the data and make it both easier to understand and to work with, we'll create two new types: a vector and a matrix. We will do a basic implementation for each which we can develop further a later date. Create a new target (not a duplicate) and call it OnTheMove. Add our two new types to the SwiftOpenGLView.swift file right after the module imports.
Vector3
Above the SwiftOpenGLView class, define a new struct called Vector3. It will have three properties, numbered 0-2. These may be used to represent x, y, z coordinates, or pitch, yaw, roll values, etc. Swift does not have an equivalent Union type per se that allows us to define types whose property names change based upon which is allocated upon creation. They do have enums which may, arguably, be an appropriate choice to implement such functionality. In the interest of staying simple, we'll just use a struct with more generic property names.
struct Vector3 {
var v0 = Float()
var v1 = Float()
var v2 = Float()
init() {}
init(v0: Float, v1: Float, v2: Float) {
self.v0 = v0
self.v1 = v1
self.v2 = v2
}
}
We want to be able to initialize a vector with default values (the values will be automatically initialized as 0.0), but we also want to be able to specify values. When we define an init( ) function, we lose the default init( ) function, so we define an empty init( ) function as you see about.
Vectors are combined in a couple ways: addition, subtraction, and multiplication. It's important to be able to visualize that is happening with the vectors when we combine them in these three ways. I recommend reviewing them before moving on. We will just move straight to implementation here.
Addition
func +(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 + rhs.v0, v1: lhs.v1 + rhs.v1, v2: lhs.v2 + rhs.v2)
}
This is an overload for the "+" operator. This definition tells the complier that if it sees a Vector3 on both sides of the operator, to add them together as defined in the closure. Vector addition is accomplished by adding the properties together and setting the sum to the properties of a new Vector3.
Subtraction
func -(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 - rhs.v0, v1: lhs.v1 - rhs.v1, v2: lhs.v2 - rhs.v2)
}
This is the same idea, but uses subtraction instead.
Multiplication
func *(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 * rhs.v0, v1: lhs.v1 * rhs.v1, v2: lhs.v2 * rhs.v2)
}
func *(lhs: Vector3, rhs: Float) -> Vector3 {
return Vector3(v0: lhs.v0 * rhs, v1: lhs.v1 * rhs, v2: lhs.v2 * rhs)
}
Again, the same idea, but notice that we have overloaded '*' twice for vector3. The second version allows us to apply a scalar to a given vector. Keep in mind that these functions must be defined at the global level. This means they are defined outside of the definition of any one type. Place there definitions above or below the Vector3 definition.
The last function we need which we shall use quite frequently, is a function to normalize a vector. This time, add the function definition within the body of Vector3.
func normalize() -> Vector3 {
let length = sqrt(v0 * v0 + v1 * v1 + v2 * v2)
return Vector3(v0: self.v0 / length, v1: self.v1 / length, v2: self.v2 / length)
}
We find the length of the vector and then create a new vector where each of the properties of the original vector have been divided by the length.
Matrix4
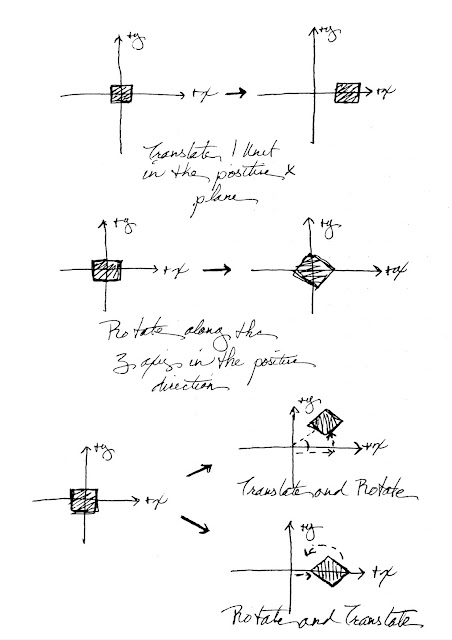
We have been displaying content in the a default Orthographic project of our model's world. Think about it. We defined our triangle in a 2x2x2 unit cube which coincides with the dimensions of the OpenGL viewing volume. Simply passing the vertex's position through to the rasterizer results in this orthographic view where no perspective has been applied. It looks like a architectural drawing. However, to make the world look more real and enable us to view a larger world, we need to be able to moved the world around. This is accomplished with matrices. We'll use them to define a camera that sits at the center of the viewing volume's 2x2x2 unit cube. Then we'll move the world in relation to the camera to simulate movement. This is part of where the math gets really dense, so we'll just talk about what each function does and how it is implemented instead of breaking down the theory behind it. The actual mathematical theory is truly necessary to understand that a translate function moves something in the x, y, and z planes and a rotate function turns something on the x, y, and z axis. The part of the theory that is import to understand is the order in which these matrices are applied. Matrices are combined by multiplication most of the time in OpenGL.
A(BC) ≠ (CB)A
If you have a translation matrix that moves 1 unit along the positive x plane and a rotation matrix that rotates along the positive z axe, you get three very different results depending on which order you multiply them.
From the above diagram, we translate and then rotate by multiplying Translate by Rotate (TR) and to rotate and then translate, we multiply Rotate by Translate (RT). Keeping the order in mind is very import when developing our app--we can reason through the results of a particular transformation.
With that said, add the Matrix4 struct definition below the Vector3 definition. It will have 16 properties. Matrices may be in a row-major or column-major order. Generally, matrices are conceptualized in row-major order where a row is filled with data before moving to the next row. OpenGL works in column major order meaning that each column is filled with data before moving to the next. Most tutorials, including those on mathematics work in row-major order, so to make our implementations easier to understand if you are looking at other tutorials on matrices, we'll implement with row-major order and then tell OpenGL to transpose the matrices when send to it to the shader. Why does OpenGL always have to be different you may ask. I don't know. There isn't any real benefit from using column-major instead of row-major, so why OpenGL decided to use a the opposite convention from everyone else is a mystery to me.
struct Matrix4 {
var m00 = Float(), m01 = Float(), m02 = Float(), m03 = Float()
var m10 = Float(), m11 = Float(), m12 = Float(), m13 = Float()
var m20 = Float(), m21 = Float(), m22 = Float(), m23 = Float()
var m30 = Float(), m31 = Float(), m32 = Float(), m33 = FLoat()
init() {
m00 = 1.0
m01 = Float()
m02 = Float()
m03 = Float()
m10 = Float()
m11 = 1.0
m12 = Float()
m13 = Float()
m20 = Float()
m21 = Float()
m22 = 1.0
m23 = Float()
m30 = Float()
m31 = Float()
m32 = Float()
m33 = 1.0
}
init(m00: Float, m01: Float, m02: Float, m03: Float,
m10: Float, m11: Float, m12: Float, m13: Float,
m20: Float, m21: Float, m22: Float, m23: Float,
m30: Float, m31: Float, m32: Float, m33: Float) {
self.m00 = m00
self.m01 = m01
self.m02 = m02
self.m03 = m03
self.m10 = m10
self.m11 = m11
self.m12 = m12
self.m13 = m13
self.m20 = m20
self.m21 = m21
self.m22 = m22
self.m23 = m23
self.m30 = m30
self.m31 = m31
self.m32 = m32
self.m33 = m33
}
init(fieldOfView for: Float, aspect: Float, nearZ: Float, farZ: Float) {
m00 = (1 / tan(fov * (M_PI / 180.0) * 0.5)) / aspect
m01 = 0.0
m02 = 0.0
m03 = 0.0
m10 = 0.0
m11 = 1 / tan(fov * (M_PI / 180.0) * 0.5)
m12 = 0.0
m13 = 0.0
m20 = 0.0
m21 = 0.0
m22 = (farZ + nearZ) / (nearZ - farZ)
m23 = (2 * farZ * nearZ) / (nearZ - farZ)
m30 = 0.0
m31 = 0.0
m32 = -1.0
m33 = 0.0
}
}
Again, we provide default initial values to the properties. We are going to make a design choice in creating the default initializer. Instead of creating a matrix where each value is zero, we will create an identity matrix upon initialization. There won't every be a time where we will need a matrix full of zeros, so creating one just to make it into an identity matrix is pointless and a waste of CPU time. In the rare instance that a matrix full of zeros is needed, we can create one with the member-wise initializer. Identity matrices do not apply transformation when multiplied with other matrices while a matrix full of zeroes destroys the transformation data held in the matrix.
A perspective matrix initializer is also supplied. The perspective matrix is what makes everything we are looking at appear to be more realistic. The fieldOfView parameter specifies how a cone that defines what is seen and what is not. It's range of appropriate values is 0.0 > x < 180.0. If you pass a value less than or equal to 0.0 or greater or equal to 180.0, the world being viewed is inverted. This value can kind of act like a zoom, but it is probably better to think of it as how large want our viewing cone to be. Zooming is better done with a scaling matrix. Also, most tutorials show the fieldOfView as a pyramid, but fieldOfView is an angle, radius, so the value actually creates a cone. The view we see is a cut-out rectangle from that cone with a ratio defined by the aspect parameter. The nearZ and farZ planes define how close and how far an object can be to be seen.
There are a couple important operations we need to perform with matrices. We need to be able to combine them with matrix multiplication, and we need to be able to create rotation and transformation matrices.
Matrix Multiplication
We'll overload the "*" operator again to accept Matrix4 times Matrix4 and also Matrix4 times Vector3.
func *(lhs: Matrix4, rhs: Matrix4) -> Matrix4 {
return Matrix4(
m00: lhs.m00 * rhs.m00 + lhs.m01 * rhs.m10 + lhs.m02 * rhs.m20 + lhs.m03 * rhs.m30,
m01: lhs.m00 * rhs.m01 + lhs.m01 * rhs.m11 + lhs.m02 * rhs.m21 + lhs.m03 * rhs.m31,
m02: lhs.m00 * rhs.m02 + lhs.m01 * rhs.m12 + lhs.m02 * rhs.m22 + lhs.m03 * rhs.m32,
m03: lhs.m00 * rhs.m03 + lhs.m01 * rhs.m13 + lhs.m02 * rhs.m23 + lhs.m03 * rhs.m33,
m10: lhs.m10 * rhs.m00 + lhs.m11 * rhs.m10 + lhs.m12 * rhs.m20 + lhs.m13 * rhs.m30,
m11: lhs.m10 * rhs.m01 + lhs.m11 * rhs.m11 + lhs.m12 * rhs.m21 + lhs.m13 * rhs.m31,
m12: lhs.m10 * rhs.m02 + lhs.m11 * rhs.m12 + lhs.m12 * rhs.m22 + lhs.m13 * rhs.m32,
m13: lhs.m10 * rhs.m03 + lhs.m11 * rhs.m13 + lhs.m12 * rhs.m23 + lhs.m13 * rhs.m33,
m20: lhs.m20 * rhs.m00 + lhs.m21 * rhs.m10 + lhs.m22 * rhs.m20 + lhs.m23 * rhs.m30,
m21: lhs.m20 * rhs.m01 + lhs.m21 * rhs.m11 + lhs.m22 * rhs.m21 + lhs.m23 * rhs.m31,
m22: lhs.m20 * rhs.m02 + lhs.m21 * rhs.m12 + lhs.m22 * rhs.m22 + lhs.m23 * rhs.m32,
m23: lhs.m20 * rhs.m03 + lhs.m21 * rhs.m13 + lhs.m22 * rhs.m23 + lhs.m23 * rhs.m33,
m30: lhs.m30 * rhs.m00 + lhs.m31 * rhs.m10 + lhs.m32 * rhs.m20 + lhs.m33 * rhs.m30,
m31: lhs.m30 * rhs.m01 + lhs.m31 * rhs.m11 + lhs.m32 * rhs.m21 + lhs.m33 * rhs.m31,
m32: lhs.m30 * rhs.m02 + lhs.m31 * rhs.m12 + lhs.m32 * rhs.m22 + lhs.m33 * rhs.m32,
m33: lhs.m30 * rhs.m03 + lhs.m31 * rhs.m13 + lhs.m32 * rhs.m23 + lhs.m33 * rhs.m33)
}
func *(lhs: Matrix4, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.m00 * rhs.v0 + lhs.m01 * rhs.v1 + lhs.m02 * rhs.v2,
v1: lhs.m10 * rhs.v0 + lhs.m11 * rhs.v1 + lhs.m12 * rhs.v2,
v2: lhs.m20 * rhs.v0 + lhs.m21 * rhs.v1 + lhs.m22 * rhs.v2)
}
To multiply two matrices, multiply the elements of the left hand side's first row element by the right hand side's first column of elements and then add these values together. This the value of the new matrices first element. Then multiply the left hand side's second row element by the right hand sides first column of element's and add these values together. Continue this process until each of the left hand side's elements have been used. Multiplying a matrix by a vector is the same process, but fewer values are processed.
The following matrix transformations are derived from Apple's GLKMath header. GLK defines it's matrices in column-major order just like what OpenGL is expecting; however, for reasons I don't understand at the moment, some of the functions work as expected with direct transcription into Swift while some require transposition. Transposition being the transformation that takes a row-major matrix and makes it a column-major matrix and vice-versa. Regardless of why, the following implementations produce the expected results. Add each of them to the bottom of the Matrix4 structure.
Inversion
To undo the transformation an given matrix has performed on a vertex, we need to apply that matrix's opposite (e.g. it's inverse). Not all matrices have an inverse, but those that do may be multiplied against their inverse to create an identity matrix. The nomenclature you may see refers to the inverse matrix as the name of the matrix with a superscript -1 (i.e. M and inverse M⁻¹). Calculating the inverse of a particular matrix is not easy feat especially when we're calculating a 4 x 4 matrix. The first step is to calculate a collection of minors. A minor is a determinant of a sub-matrix from the given matrix. A determinant, for a 2 x 2 matrix is calculated by cross multiplying and ten subtracting these products. For a 3 x 3 matrix, select the element of the first column and row. Now excluding elements in this column and row, notice that a 2 x 2 matrix are created. Now cross-multiply and subtract the products just as before. Using this sum, multiply it by the element in the first column and row. This is the first minor. Repeat this process for the each of the elements. Once you have these values, take the top row and place them in parentheses. Outside of the parentheses, place alternating signs (i.e. +(-x) -(y) +(z), notice that I purposely place a '-' in front of the x to show that these signs should applied to the value such that '--' would make a value positive as expected). Combine according to their sign--we have the determinant. To get the inverse of a matrix, we need the inverse determinant, so divide '1' by the determinant. Now apply the same sign convention to the whole matrix such the row's and column's alternate (i.e. + - + -, etc.). Now transpose the matrix (i.e. consider the rows going from left to right as columns going from top to bottom). Finally, multiply each of the elements in this minors collection by the determinant. With that we have an inverse matrix.
func inverse() -> Matrix4 {
// Capture the current matrix
let m = self
// Calculate the minors of self
let minors = Matrix4(
m00: (m.m11 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m12 * (m.m21 * m.m33 - m.m23 *
➥ m.m31)) + (m.m13 * (m.m21 * m.m32 - m.m22 * m.m31)),
m01: (m.m10 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m12 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m13 * (m.m20 * m.m32 - m.m22 * m.m30)),
m02: (m.m10 * (m.m21 * m.m33 - m.m23 * m.m31)) - (m.m11 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m13 * (m.m20 * m.m31 - m.m21 * m.m30)),
m03: (m.m10 * (m.m21 * m.m32 - m.m22 * m.m31)) - (m.m11 * (m.m20 * m.m32 - m.m22 *
➥ m.m30)) + (m.m12 * (m.m20 * m.m31 - m.m21 * m.m30)),
m10: (m.m01 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m02 * (m.m21 * m.m33 - m.m23 *
➥ m.m31)) + (m.m03 * (m.m21 * m.m32 - m.m22 * m.m31)),
m11: (m.m00 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m02 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m03 * (m.m20 * m.m32 - m.m22 * m.m30)),
m12: (m.m00 * (m.m21 * m.m33 - m.m23 * m.m31)) - (m.m01 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m03 * (m.m20 * m.m31 - m.m21 * m.m30)),
m13: (m.m00 * (m.m21 * m.m32 - m.m22 * m.m31)) - (m.m01 * (m.m20 * m.m32 - m.m22 *
➥ m.m30)) + (m.m02 * (m.m20 * m.m31 - m.m21 * m.m30)),
m20: (m.m01 * (m.m12 * m.m33 - m.m13 * m.m32)) - (m.m02 * (m.m11 * m.m33 - m.m13 *
➥ m.m31)) + (m.m03 * (m.m11 * m.m32 - m.m12 * m.m31)),
m21: (m.m00 * (m.m12 * m.m33 - m.m13 * m.m32)) - (m.m02 * (m.m10 * m.m33 - m.m13 *
➥ m.m30)) + (m.m03 * (m.m10 * m.m32 - m.m12 * m.m30)),
m22: (m.m00 * (m.m11 * m.m33 - m.m13 * m.m31)) - (m.m01 * (m.m10 * m.m33 - m.m13 *
➥ m.m30)) + (m.m03 * (m.m10 * m.m31 - m.m11 * m.m30)),
m23: (m.m00 * (m.m11 * m.m32 - m.m12 * m.m31)) - (m.m01 * (m.m10 * m.m32 - m.m12 *
➥ m.m30)) + (m.m02 * (m.m10 * m.m31 - m.m11 * m.m30)),
m30: (m.m01 * (m.m12 * m.m23 - m.m13 * m.m22)) - (m.m02 * (m.m11 * m.m23 - m.m13 *
➥ m.m21)) + (m.m03 * (m.m11 * m.m22 - m.m12 * m.m21)),
m31: (m.m00 * (m.m12 * m.m23 - m.m13 * m.m22)) - (m.m02 * (m.m10 * m.m23 - m.m13 *
➥ m.m20)) + (m.m03 * (m.m10 * m.m22 - m.m12 * m.m20)),
m32: (m.m00 * (m.m11 * m.m23 - m.m13 * m.m21)) - (m.m01 * (m.m10 * m.m23 - m.m13 *
➥ m.m20)) + (m.m03 * (m.m10 * m.m21 - m.m11 * m.m20)),
m33: (m.m00 * (m.m11 * m.m22 - m.m12 * m.m21)) - (m.m01 * (m.m10 * m.m22 - m.m12 *
➥ m.m20)) + (m.m02 * (m.m10 * m.m21 - m.m11 * m.m20)))
// Calculate the inverse determinant by multiplying the elements of the first row
// of self by the elements of the first row of minors then get the reciprocal
let invDeterminant = 1 / (m.m00 * minors.m00 - m.m01 * minors.m01 + m.m02 * minors.m02 -
➥ m.m03 * minors.m03)
// Apply the + - sign pattern, transpose the matrix, then multiply by the invDeterminant
let im = Matrix4(
m00: +minors.m00 * invDeterminant,
m01: -minors.m10 * invDeterminant,
m02: +minors.m20 * invDeterminant,
m03: -minors.m30 * invDeterminant,
m10: -minors.m01 * invDeterminant,
m11: +minors.m11 * invDeterminant,
m12: -minors.m21 * invDeterminant,
m13: +minors.m31 * invDeterminant,
m20: +minors.m02 * invDeterminant,
m21: -minors.m12 * invDeterminant,
m22: +minors.m22 * invDeterminant,
m23: -minors.m32 * invDeterminant,
m30: -minors.m03 * invDeterminant,
m31: +minors.m13 * invDeterminant,
m32: -minors.m23 * invDeterminant,
m33: +minors.m33 * invDeterminant)
return im
}
Translation
The last column of a matrix decides the amount of translation. For instance, moving along the z plane (forward or backward within the 3D world) is as easy as setting the z component of this vector (the third value down in the fourth column). A more accurate matrix takes the first column (the x vector), and sets the sum of those products to the fourth column's x value (the first value in the fourth column). The second column (the y Vector) and the third column (the z vector) are treated in the same way. Our translation matrix implementation:
func translate(x x: Float, y: Float, z: Float) -> Matrix4 {
var m = Matrix4()
m.m03 += m.m00 * x + m.m01 * y + m.m02 * z
m.m13 += m.m10 * x + m.m11 * y + m.m12 * z
m.m23 += m.m20 * x + m.m21 * y + m.m22 * z
m.m33 += m.m30 * x + m.m31 * y + m.m32 * z
return self * m
}
Rotation
We shall implement three rotation matrices. We really only need to implement one of the three or two of the three to get the results we want, but I feel it is useful to look at both methods. The first, in which we could implement just one rotation method, allows us to rotate about any arbitrary axis. We just pass in a unit vector and a degree of rotation in radians.
func rotate(radians angle: Float, alongAxis axis: Vector3) -> Matrix4 {
let cosine = cos(angle)
let inverseCosine = 1.0 - cosine
let sine = sin(angle)
return self * Matrix4(
m00: cosine + inverseCosine * axis.v0 * axis.v0,
m01: inverseCosine * axis.v0 * axis.v1 + axis.v2 * sine,
m02: inverseCosine * axis.v0 * axis.v2 - axis.v1 * sine,
m03: 0.0,
m10: inverseCosine * axis.v0 * axis.v1 - axis.v2 * sine,
m11: cosine + inverseCosine * axis.v1 * axis.v1,
m12: inverseCosine * axis.v1 * axis.v2 + axis.v0 * sine,
m13: 0.0,
m20: inverseCosine * axis.v0 * axis.v2 + axis.v1 * sine,
m21: inverseCosine * axis.v1 * axis.v2 - axis.v0 * sine,
m22: cosine + inverseCosine * axis.v2 * axis.v2,
m23: 0.0,
m30: 0.0,
m31: 0.0,
m32: 0.0,
m33: 1.0)
}
Obviously, a very useful function, but it takes several computations to compute. In contrast, if we set a prerequisite that we are going to rotate about a particular axis such as the x or y, then the computation is greatly simplified. For rotation about the x axis:
func rotateAlongXAxis(radians: Float) -> Matrix4 {
var m = Matrix4()
m.m11 = cos(radians)
m.m12 = sin(radians)
m.m21 = -sin(radians)
m.m22 = cos(radians)
return self * m
}
For rotation about the y axis:
func rotateAlongYAxis(radians: Float) -> Matrix4 {
var m = Matrix4()
m.m00 = cos(radians)
m.m02 = -sin(radians)
m.m20 = sin(radians)
m.m22 = cos(radians)
return self * m
}
When working with rotation, you have to know that the axes themselves rotation when the model is rotated. This becomes really important when implementing a camera that orbits about a point in space. Rotating an object on the y axis, and then rotating on the x axis results in the object adjusting it's pitch according to the object's local space. To get the object to adjust pitch according the view's space, you need to calculate what the view's x axis vector is in terms of the object's local space after being rotated on the y axis. Confusing? Yes, but don't worry about it for now, we'll get to that later.
The last function we'll need for our matrix creates an array that can be passed to OpenGL. Unfortunately OpenGL doesn't accept our structs because it is not a pointer to a GLfloat or an array of GLfloats. In order to pass the struct to OpenGL, our function will return our struct in the form of an array literal. As an added bonus, it will transpose the data going into the array so that OpenGL doesn't have to do any extra work (recall that the OpenGL attribute pointer functions provide a transpose option for matrices). Note the ordering of the data below--it's passing in each column after the other (column-major order) instead of each row after the other (row-major order).
func asArray() -> [Float] {
return [self.m00, self.m10, self.m20, self.m30,
self.m01, self.m11, self.m21, self.m31,
self.m02, self.m12, self.m22, self.m32,
self.m03, self.m13, self.m23, self.m33]
}
The full implementation of Vector3 and Matrix4 are below and should be added to the top of the SwiftOpenGLView.swift file after the import's.
func *(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 * rhs.v0, v1: lhs.v1 * rhs.v1, v2: lhs.v2 * rhs.v2)
}
func *(lhs: Vector3, rhs: Float) -> Vector3 {
return Vector3(v0: lhs.v0 * rhs, v1: lhs.v1 * rhs, v2: lhs.v2 * rhs)
}
func +(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 + rhs.v0, v1: lhs.v1 + rhs.v1, v2: lhs.v2 + rhs.v2)
}
func -(lhs: Vector3, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.v0 - rhs.v0, v1: lhs.v1 - rhs.v1, v2: lhs.v2 - rhs.v2)
}
struct Vector3 {
var v0 = Float()
var v1 = Float()
var v2 = Float()
init() {}
init(v0: Float, v1: Float, v2: Float) {
self.v0 = v0
self.v1 = v1
self.v2 = v2
}
func normalize() -> Vector3 {
let length = sqrt(v0 * v0 + v1 * v1 + v2 * v2)
return Vector3(v0: self.v0 / length, v1: self.v1 / length, v2: self.v2 / length)
}
}
func ==(lhs: Matrix4, rhs: Matrix4) -> Bool {
return lhs.hashValue == rhs.hashValue
}
func *(lhs: Matrix4, rhs: Matrix4) -> Matrix4 {
return Matrix4(
m00: lhs.m00 * rhs.m00 + lhs.m01 * rhs.m10 + lhs.m02 * rhs.m20 + lhs.m03 * rhs.m30,
m01: lhs.m00 * rhs.m01 + lhs.m01 * rhs.m11 + lhs.m02 * rhs.m21 + lhs.m03 * rhs.m31,
m02: lhs.m00 * rhs.m02 + lhs.m01 * rhs.m12 + lhs.m02 * rhs.m22 + lhs.m03 * rhs.m32,
m03: lhs.m00 * rhs.m03 + lhs.m01 * rhs.m13 + lhs.m02 * rhs.m23 + lhs.m03 * rhs.m33,
m10: lhs.m10 * rhs.m00 + lhs.m11 * rhs.m10 + lhs.m12 * rhs.m20 + lhs.m13 * rhs.m30,
m11: lhs.m10 * rhs.m01 + lhs.m11 * rhs.m11 + lhs.m12 * rhs.m21 + lhs.m13 * rhs.m31,
m12: lhs.m10 * rhs.m02 + lhs.m11 * rhs.m12 + lhs.m12 * rhs.m22 + lhs.m13 * rhs.m32,
m13: lhs.m10 * rhs.m03 + lhs.m11 * rhs.m13 + lhs.m12 * rhs.m23 + lhs.m13 * rhs.m33,
m20: lhs.m20 * rhs.m00 + lhs.m21 * rhs.m10 + lhs.m22 * rhs.m20 + lhs.m23 * rhs.m30,
m21: lhs.m20 * rhs.m01 + lhs.m21 * rhs.m11 + lhs.m22 * rhs.m21 + lhs.m23 * rhs.m31,
m22: lhs.m20 * rhs.m02 + lhs.m21 * rhs.m12 + lhs.m22 * rhs.m22 + lhs.m23 * rhs.m32,
m23: lhs.m20 * rhs.m03 + lhs.m21 * rhs.m13 + lhs.m22 * rhs.m23 + lhs.m23 * rhs.m33,
m30: lhs.m30 * rhs.m00 + lhs.m31 * rhs.m10 + lhs.m32 * rhs.m20 + lhs.m33 * rhs.m30,
m31: lhs.m30 * rhs.m01 + lhs.m31 * rhs.m11 + lhs.m32 * rhs.m21 + lhs.m33 * rhs.m31,
m32: lhs.m30 * rhs.m02 + lhs.m31 * rhs.m12 + lhs.m32 * rhs.m22 + lhs.m33 * rhs.m32,
m33: lhs.m30 * rhs.m03 + lhs.m31 * rhs.m13 + lhs.m32 * rhs.m23 + lhs.m33 * rhs.m33)
}
func *(lhs: Matrix4, rhs: Vector3) -> Vector3 {
return Vector3(v0: lhs.m00 * rhs.v0 + lhs.m01 * rhs.v1 + lhs.m02 * rhs.v2,
v1: lhs.m10 * rhs.v0 + lhs.m11 * rhs.v1 + lhs.m12 * rhs.v2,
v2: lhs.m20 * rhs.v0 + lhs.m21 * rhs.v1 + lhs.m22 * rhs.v2)
}
struct Matrix4 {
var m00 = Float(), m01 = Float(), m02 = Float(), m03 = Float()
var m10 = Float(), m11 = Float(), m12 = Float(), m13 = Float()
var m20 = Float(), m21 = Float(), m22 = Float(), m23 = Float()
var m30 = Float(), m31 = Float(), m32 = Float(), m33 = Float()
init() {
m00 = 1.0
m01 = Float()
m02 = Float()
m03 = Float()
m10 = Float()
m11 = 1.0
m12 = Float()
m13 = Float()
m20 = Float()
m21 = Float()
m22 = 1.0
m23 = Float()
m30 = Float()
m31 = Float()
m32 = Float()
m33 = 1.0
}
init(m00: Float, m01: Float, m02: Float, m03: Float,
m10: Float, m11: Float, m12: Float, m13: Float,
m20: Float, m21: Float, m22: Float, m23: Float,
m30: Float, m31: Float, m32: Float, m33: Float) {
self.m00 = m00
self.m01 = m01
self.m02 = m02
self.m03 = m03
self.m10 = m10
self.m11 = m11
self.m12 = m12
self.m13 = m13
self.m20 = m20
self.m21 = m21
self.m22 = m22
self.m23 = m23
self.m30 = m30
self.m31 = m31
self.m32 = m32
self.m33 = m33
}
init(fieldOfView fov: Float, aspect: Float, nearZ: Float, farZ: Float) {
m00 = (1 / tanf(fov * (Float(M_PI) / 180.0) * 0.5)) / aspect
m01 = 0.0
m02 = 0.0
m03 = 0.0
m10 = 0.0
m11 = 1 / tanf(fov * (Float(M_PI) / 180.0) * 0.5)
m12 = 0.0
m13 = 0.0
m20 = 0.0
m21 = 0.0
m22 = (farZ + nearZ) / (nearZ - farZ)
m23 = (2 * farZ * nearZ) / (nearZ - farZ)
m30 = 0.0
m31 = 0.0
m32 = -1.0
m33 = 0.0
}
func asArray() -> [Float] {
return [self.m00, self.m10, self.m20, self.m30,
self.m01, self.m11, self.m21, self.m31,
self.m02, self.m12, self.m22, self.m32,
self.m03, self.m13, self.m23, self.m33]
}
func inverse() -> Matrix4 {
let m = self
let minors = Matrix4(
m00: (m.m11 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m12 * (m.m21 * m.m33 - m.m23 *
➥ m.m31)) + (m.m13 * (m.m21 * m.m32 - m.m22 * m.m31)),
m01: (m.m10 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m12 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m13 * (m.m20 * m.m32 - m.m22 * m.m30)),
m02: (m.m10 * (m.m21 * m.m33 - m.m23 * m.m31)) - (m.m11 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m13 * (m.m20 * m.m31 - m.m21 * m.m30)),
m03: (m.m10 * (m.m21 * m.m32 - m.m22 * m.m31)) - (m.m11 * (m.m20 * m.m32 - m.m22 *
➥ m.m30)) + (m.m12 * (m.m20 * m.m31 - m.m21 * m.m30)),
m10: (m.m01 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m02 * (m.m21 * m.m33 - m.m23 *
➥ m.m31)) + (m.m03 * (m.m21 * m.m32 - m.m22 * m.m31)),
m11: (m.m00 * (m.m22 * m.m33 - m.m23 * m.m32)) - (m.m02 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m03 * (m.m20 * m.m32 - m.m22 * m.m30)),
m12: (m.m00 * (m.m21 * m.m33 - m.m23 * m.m31)) - (m.m01 * (m.m20 * m.m33 - m.m23 *
➥ m.m30)) + (m.m03 * (m.m20 * m.m31 - m.m21 * m.m30)),
m13: (m.m00 * (m.m21 * m.m32 - m.m22 * m.m31)) - (m.m01 * (m.m20 * m.m32 - m.m22 *
➥ m.m30)) + (m.m02 * (m.m20 * m.m31 - m.m21 * m.m30)),
m20: (m.m01 * (m.m12 * m.m33 - m.m13 * m.m32)) - (m.m02 * (m.m11 * m.m33 - m.m13 *
➥ m.m31)) + (m.m03 * (m.m11 * m.m32 - m.m12 * m.m31)),
m21: (m.m00 * (m.m12 * m.m33 - m.m13 * m.m32)) - (m.m02 * (m.m10 * m.m33 - m.m13 *
➥ m.m30)) + (m.m03 * (m.m10 * m.m32 - m.m12 * m.m30)),
m22: (m.m00 * (m.m11 * m.m33 - m.m13 * m.m31)) - (m.m01 * (m.m10 * m.m33 - m.m13 *
➥ m.m30)) + (m.m03 * (m.m10 * m.m31 - m.m11 * m.m30)),
m23: (m.m00 * (m.m11 * m.m32 - m.m12 * m.m31)) - (m.m01 * (m.m10 * m.m32 - m.m12 *
➥ m.m30)) + (m.m02 * (m.m10 * m.m31 - m.m11 * m.m30)),
m30: (m.m01 * (m.m12 * m.m23 - m.m13 * m.m22)) - (m.m02 * (m.m11 * m.m23 - m.m13 *
➥ m.m21)) + (m.m03 * (m.m11 * m.m22 - m.m12 * m.m21)),
m31: (m.m00 * (m.m12 * m.m23 - m.m13 * m.m22)) - (m.m02 * (m.m10 * m.m23 - m.m13 *
➥ m.m20)) + (m.m03 * (m.m10 * m.m22 - m.m12 * m.m20)),
m32: (m.m00 * (m.m11 * m.m23 - m.m13 * m.m21)) - (m.m01 * (m.m10 * m.m23 - m.m13 *
➥ m.m20)) + (m.m03 * (m.m10 * m.m21 - m.m11 * m.m20)),
m33: (m.m00 * (m.m11 * m.m22 - m.m12 * m.m21)) - (m.m01 * (m.m10 * m.m22 - m.m12 *
➥ m.m20)) + (m.m02 * (m.m10 * m.m21 - m.m11 * m.m20)))
let invDeterminant = 1 / (m.m00 * minors.m00 - m.m01 * minors.m01 + m.m02 * minors.m02 -
➥ m.m03 * minors.m03)
let im = Matrix4(
m00: +minors.m00 * invDeterminant,
m01: -minors.m10 * invDeterminant,
m02: +minors.m20 * invDeterminant,
m03: -minors.m30 * invDeterminant,
m10: -minors.m01 * invDeterminant,
m11: +minors.m11 * invDeterminant,
m12: -minors.m21 * invDeterminant,
m13: +minors.m31 * invDeterminant,
m20: +minors.m02 * invDeterminant,
m21: -minors.m12 * invDeterminant,
m22: +minors.m22 * invDeterminant,
m23: -minors.m32 * invDeterminant,
m30: -minors.m03 * invDeterminant,
m31: +minors.m13 * invDeterminant,
m32: -minors.m23 * invDeterminant,
m33: +minors.m33 * invDeterminant)
return im
}
func translate(x x: Float, y: Float, z: Float) -> Matrix4 {
var m = Matrix4()
m.m03 += m.m00 * x + m.m01 * y + m.m02 * z
m.m13 += m.m10 * x + m.m11 * y + m.m12 * z
m.m23 += m.m20 * x + m.m21 * y + m.m22 * z
m.m33 += m.m30 * x + m.m31 * y + m.m32 * z
return self * m
}
func rotateAlongXAxis(radians: Float) -> Matrix4 {
var m = Matrix4()
m.m11 = cos(radians)
m.m12 = sin(radians)
m.m21 = -sin(radians)
m.m22 = cos(radians)
return self * m
}
func rotateAlongYAxis(radians: Float) -> Matrix4 {
var m = Matrix4()
m.m00 = cos(radians)
m.m02 = -sin(radians)
m.m20 = sin(radians)
m.m22 = cos(radians)
return self * m
}
func rotate(radians angle: Float, alongAxis axis: Vector3) -> Matrix4 {
let cosine = cos(angle)
let inverseCosine = 1.0 - cosine
let sine = sin(angle)
return self * Matrix4(
m00: cosine + inverseCosine * axis.v0 * axis.v0,
m01: inverseCosine * axis.v0 * axis.v1 + axis.v2 * sine,
m02: inverseCosine * axis.v0 * axis.v2 - axis.v1 * sine,
m03: 0.0,
m10: inverseCosine * axis.v0 * axis.v1 - axis.v2 * sine,
m11: cosine + inverseCosine * axis.v1 * axis.v1,
m12: inverseCosine * axis.v1 * axis.v2 + axis.v0 * sine,
m13: 0.0,
m20: inverseCosine * axis.v0 * axis.v2 + axis.v1 * sine,
m21: inverseCosine * axis.v1 * axis.v2 - axis.v0 * sine,
m22: cosine + inverseCosine * axis.v2 * axis.v2,
m23: 0.0,
m30: 0.0,
m31: 0.0,
m32: 0.0,
m33: 1.0)
}
}
Now that we have our types defined, we can move on to creating a camera system to use them. We'll cover some basic keyboard and mouse input and you'll see one way of communicating between a view controller and a view. Understanding the separation between view controllers and views is vital to understanding part of Apple's conformance to MVC design (Model-View-Controller). We'll cover more of that topic in the future, but first things first.
Thank you for reading! If you have any comments, please leave them below! Help to make these tutorials better would be greatly appreciated.
When you are ready, click here to finish implementing our OpenGL Camera.
Thank you for reading! If you have any comments, please leave them below! Help to make these tutorials better would be greatly appreciated.
When you are ready, click here to finish implementing our OpenGL Camera.



Really enjoyed these, they have been very useful.
ReplyDeleteWhen's the next one due?
Thank you, I'm glad that you enjoyed the posts! I'm working on the second part for this one now. My apologies for the delay. Generally, I try to do a post each weekend to every other weekend, but work has been keeping me busy.
DeleteIf there is every something doesn't make sense, or doesn't work, please just let me know. I'll try to explain it better or fix the problem. Thank you, again for the comment.
Thanks.
DeleteEverything has made sense so far, but we are just getting into the complicated stuff! I've just had to tweak things to make it work in swift2 but no big deal.
Excellent, thank you for pointing that out! I went back and made sure each of the projects is compiling in Swift 2.1. Each of the tutorials should now compile without errors.
DeleteHi Myles,
ReplyDeleteI'm working my way through this and creating an xCode project like yours with multiple targets. In doing so I've found a number of small typos in the code. I'll list them here; the original line first followed by the corrected line.
Tutorial 0.1
guard let pixelFormat = NSOpenGLPixelFormat(attributes: attires) else {
guard let pixelFormat = NSOpenGLPixelFormat(attributes: attrs) else {
let context = NSOpenGLContext(format: pixelFormat, shareContext: nil) else {
guard let context = NSOpenGLContext(format: pixelFormat, shareContext: nil) else {
Tutorial 2.2
var textureData = UnsafeMutablePointer(malloc(256 * 4 * 256))
let textureData = UnsafeMutablePointer(malloc(256 * 4 * 256))
Tutorial 2.3
glBufferData(GLenum(GL_ARRAY_BUFFER), data.count * sizeof(Vertex), data, GLenum(GL_STATIC_DRAW))
glBufferData(GLenum(GL_ARRAY_BUFFER), data.count * sizeof(GLfloat), data, GLenum(GL_STATIC_DRAW))
Tutorial 2.4
let data [GLfloat] = [-1.0, -1.0, 1.0, 0.0, 1.0, 0.0, 2.0, -1.0, -1.0, 0.0001,
let data: [GLfloat] = [-1.0, -1.0, 1.0, 0.0, 1.0, 0.0, 2.0, -1.0, -1.0, 0.0001,
Tutorial 3.0
" float specular = pow(max(dot(viewer, reflection), 0.0),
➥ ight.specHardness); \n" +
" float specular = pow(max(dot(viewer, reflection), 0.0),
➥ light.specHardness); \n" +
" vec3 light = light.ambient + light.color * intensity +
➥ ight.specStrength * specular * light.color; \n" +
" vec3 light = light.ambient + light.color * intensity +
➥ light.specStrength * specular * light.color; \n" +
Swift.print("Could not compile fragement, getting log")
Swift.print("Could not compile fragment, getting log")
This last one is more serious, the hashValue func isn't included in the code.
Tutorial 3.1
func ==(lhs: Matrix4, rhs: Matrix4) -> Bool {
return lhs.hashValue == rhs.hashValue
}
So far I've been able to get everything up to and including 3.0 to compile and run.
Doug
Thank you for the edits. I've fixed them. In regard to the function "==", I purposely did not include it in the tutorial as it was not used in the code above or in successive tutorials at this point. I would have made the Matrix4 struct conform to equitable and hashable if I were going to introduce this function. I realize you have been using these tutorials to help supplement some elements of an existing project of your own, so you may have required this function. However, I'm doing my best to write these tutorials in a way that someone new to OpenGL can follow along by building the exact project that I am building and then experiment with it at their leisure. I'm doing this so I don't get ahead of the covered data. I'll cover protocols like hashable at a later time when we need to see if two types are equal. For now, I'm just including the necessary functions.
ReplyDelete