2.3: Shedding Some Light On the Scene
In OpenGL, lighting a 3D scene can become a very complex undertaking. In the previous tutorials, our lighting system was very simple: we assigned a color to a fragment based upon the interpolated color and/or texture. This lighting model assumed all surfaces are faced directly by a light source. This method of lighting is certainly cheap computationally, but it is highly unrealistic.
To create a more realistic lighting model, we'll need to define what is a lit surface and what is a dark surface. We can say that any point on a surface has a lit value that falls between 0.0 and 1.0 where 0.0 is fully in shadow and 1.0 is fully lit. Light that doesn't touch the surface (light at <= 0 degrees to the surface which would be parallel or beneath the surface) is full shadow while light at 90 degrees to the surface makes a surface fully lit. Finally, light at any angle >0.0 and <90.0 results in a surface lighting value >0.0 but < 1.0. This lighting model essentially assumes that the model surface is a simple, entirely convex shape not obstructed by any other surface that would normally cause a shadow. However, the problem we have now is, how do we know which way the surface is facing?
The normal is a vector rationalized as being located at the center of a surface and perpendicular to it (denoted by N in the figure below). The normal will be our reference uncalculating the direction a surface is facing. In the figure below, N is the normal vector, theta is the angle between the normal and the light vector l below.
To calculate the amount that a surface is lit (a value between 0.0-1.0), we will use some trigonometry. First, the dot product calculates a scalar value that is positive when the angle between two vectors is less that 90 degrees, zero when the angle is 90 degrees, and negative when the angle is greater than 90 degrees. The dot product essentially tells us the general orientation of two vectors to one another. The dot product is equal to the sum of the x, y, and z values of one vector multiplied by the x, y, and z values of the other vector. The notation for the dot product is " ⋅ ".
A ⋅ B = Ax(Bx) + Ay(By) + Az(Bz)
However, there is another definition of the dot product that utilizes cosine of the angle between the two vectors. This definition of the dot product is equal to the product of the magnitude of of A multiplied by the magnitude of B multiplied by the cosine of the angle between vectors A and B.
A ⋅ B = |A||B|cos𝛉 (where "| |" is the magnitude, or length, of a vector).
Our lighting model is based upon the angle between the light ray approaching the surface and the normal of the surface, but we want this angle described in terms of a value from 0.0-1.0. The cosine of an angle gives us just such a value. Cos𝛉 gives us that value. We can use both definitions of the dot product to calculate cos𝛉.
cos𝛉 = A ⋅ B / |A||B|
Note that we aren't looking for the actual angle (the arccosine). When we translate this value into GLSL code, we can use too GLSL functions dot() (which calculates the dot product), and length() (which calculates the length of a vector). There is an easy optimization that we can make here. If the vectors passed into this equation are normalized unit vectors, we can simplify the equation to
cos𝛉 = A ⋅ B
This is because multiplying two unit vectors together and then dividing by the product is equivalent to dividing by one.
The new fragment shader code below uses the above ideas to calculate if a surface is lit and by how much.
To create a more realistic lighting model, we'll need to define what is a lit surface and what is a dark surface. We can say that any point on a surface has a lit value that falls between 0.0 and 1.0 where 0.0 is fully in shadow and 1.0 is fully lit. Light that doesn't touch the surface (light at <= 0 degrees to the surface which would be parallel or beneath the surface) is full shadow while light at 90 degrees to the surface makes a surface fully lit. Finally, light at any angle >0.0 and <90.0 results in a surface lighting value >0.0 but < 1.0. This lighting model essentially assumes that the model surface is a simple, entirely convex shape not obstructed by any other surface that would normally cause a shadow. However, the problem we have now is, how do we know which way the surface is facing?
The normal is a vector rationalized as being located at the center of a surface and perpendicular to it (denoted by N in the figure below). The normal will be our reference uncalculating the direction a surface is facing. In the figure below, N is the normal vector, theta is the angle between the normal and the light vector l below.
To calculate the amount that a surface is lit (a value between 0.0-1.0), we will use some trigonometry. First, the dot product calculates a scalar value that is positive when the angle between two vectors is less that 90 degrees, zero when the angle is 90 degrees, and negative when the angle is greater than 90 degrees. The dot product essentially tells us the general orientation of two vectors to one another. The dot product is equal to the sum of the x, y, and z values of one vector multiplied by the x, y, and z values of the other vector. The notation for the dot product is " ⋅ ".
A ⋅ B = Ax(Bx) + Ay(By) + Az(Bz)
However, there is another definition of the dot product that utilizes cosine of the angle between the two vectors. This definition of the dot product is equal to the product of the magnitude of of A multiplied by the magnitude of B multiplied by the cosine of the angle between vectors A and B.
A ⋅ B = |A||B|cos𝛉 (where "| |" is the magnitude, or length, of a vector).
Our lighting model is based upon the angle between the light ray approaching the surface and the normal of the surface, but we want this angle described in terms of a value from 0.0-1.0. The cosine of an angle gives us just such a value. Cos𝛉 gives us that value. We can use both definitions of the dot product to calculate cos𝛉.
cos𝛉 = A ⋅ B / |A||B|
Note that we aren't looking for the actual angle (the arccosine). When we translate this value into GLSL code, we can use too GLSL functions dot() (which calculates the dot product), and length() (which calculates the length of a vector). There is an easy optimization that we can make here. If the vectors passed into this equation are normalized unit vectors, we can simplify the equation to
cos𝛉 = A ⋅ B
This is because multiplying two unit vectors together and then dividing by the product is equivalent to dividing by one.
The new fragment shader code below uses the above ideas to calculate if a surface is lit and by how much.
"#version 330 core \n" +
"uniform sampler2D sample; \n" +
/ 1 "uniform vec3 lightColor; \n" +
/ 2 "uniform vec3 lightPosition; \n" +
/ 3 "in vec3 passPosition; \n" +
"in vec3 passColor; \n" +
"in vec2 passTexturePosition; \n" +
/ 4 "in vec3 passNormal; \n" +
"out vec4 outColor; \n" +
"void main() \n" +
"{ \n" +
/ 5 " vec3 normal = normalize(passNormal); \n" +
/ 6 " vec3 lightRay = normalize(lightPosition - passPosition); \n" +
/ 7 " float intensity = dot(normal, lightRay) / (length(normal) * length(lightRay)); \n" +
/ 8 " intensity = clamp(intensity, 0, 1); \n" +
/ 9 " vec3 light = lightColor * intensity; \n" +
/10 " vec3 surface = texture(sample, passTexturePosition).rgb * passColor; \n" +
/11 " vec3 rgb = surface * light; \n" +
/12 " outColor = vec4(rgb, 1.0); \n" +
"} \n"
Each new line has a number next to it for reference. Lines 1-4 are new variables for use within the shader. 1 and 2 are values that represent aspects of the light source. The light has a color and a position and each are represented by three elements--r, g, b and x, y, z. Note that we are using three elements to present the light position instead of two. This is to make it a little easier to understand the position of the light as we make adjustments and see the effects. 3 is the interpolated position of the vertex. This might be a little hard to wrap your head around at first, but the passPosition (even though we will have set this to the vertex position in the vertex shader) is an interpolated value in the fragment shader that lies somewhere within or along the area of that particular primitive. This is the exact same idea as the texture position, but somehow, that's seems easier to understand though.
4 is another interpolated value, this time the normal. We are drawing only one primitive to the screen, so we should really only have one normal. However, this is not going to produce a very interesting effect as the every point on the surface will be point the same direction and have the same lit value.
Instead we're going to cheat and make OpenGL think that there is more geometry to this triangle than there truly is. We will do this by passing a different normal for each vertex.
In the figure above, we define three normals of unit length (length equal to 1.0). The location of the normal is not what is important, it is the direction it points! When you work with passNormal, you're getting an interpolated value amount the normals within a primitive. This interpolation is linear which means that the passNormal is pointing in the right direction, but is usually not of unit length. That's why we renormalize each passNormal to get the true normal for that fragment as in line 5 above.
Line 6 is where we get the other vector, the light ray vector, that we will use in our calculation of the the cos𝛉. It's really important that subtract the appropriate vector from the other so you don't get the exact opposite lighting effect you intended. Here, lightPosition points from the origin to the light's position and passPosition (the interpolated position of the vertices upon the surface) points in the same direction. Generally, the passPosition is going to be shorter than the lightPosition. That means we want to subtract the passPosition from the lightPosition and not the other way around so that we end up with a vector pointing in the right direction--the same direction as the light. This vector should also be normalized before we use it in our cos𝛉 calculation.
Line 7 is where we calculate the intensity of light at that point on the surface using our cos𝛉 calculation. This value is not guaranteed to be between 0.0 and 1.0 so we use clamp() (line 8). We could also use an if statement, but I feel clamp() is more readable.
Line 9 encapsulates the lights effect. This variable will later all hold information about the ambient and specular components of light. For now it is purely affected by the diffuse component.
Line 10's surface variable definition is just a renaming of the variable that encapsulates the model's color at this fragment. It includes texture and vertex color components, but it otherwise unchanged.
Line 11 is the calculated color of the fragment once the light and surface components are combined. You could do the same within line 12, but separating it out takes less horizontal space for the blog and perhaps reads a little better as well. Regardless, line 12 is the final color of the fragment with the alpha component appended.
We have a new component that we need to add to our vertex--the normal. The new data definition layout shall be: x, y, r, g, b, s, t, nx, ny, nz.
In the above array, I have defined the normals as pointing every so slightly in the positive z direction. Note that this makes them inherently not normalized, but since we're going to be using normalize() on each normal each time, it doesn't really matter. I made them point in the positive Z direction to give OpenGL a hint that the normal at the center of the triangle is supposed to point straight at the viewer instead of away. What we end up with is a triangle with normals like this.
The normals result an a sort of pointed surface like a cone. Even though the triangle itself is flat, these normals cause the surface to appear to have a three dimensional shape. This is the basis for bump and normal maps.
We need to add the appropriate vertex attribute as well. Our vertex is now 40 bytes and the normal attribute is, itself, 12 bytes located after the texture coordinate information (28 bytes from the address of the vertex).
We'll also need to add the corresponding in and out attributes to the vertex shader. The position attribute will be passed to the fragment shader through the passPosition and the normal will be passed through the passNormal.
We also have to add new uniforms for the light. Unlike the texture sampler uniform, these uniforms must be defined after a program is activated. We are going to define a light that casts white light and shines from the top of triangle.
The 3fv indicates 3 components of type float passed as a vector. The function's second parameter "size" is the number of vectors you are sending, not the number of components. We are sending an array of vectors with a count of 1 in each case.
Those are some of the highlights of the code. Below, is the full class implementation with comments.
4 is another interpolated value, this time the normal. We are drawing only one primitive to the screen, so we should really only have one normal. However, this is not going to produce a very interesting effect as the every point on the surface will be point the same direction and have the same lit value.
Instead we're going to cheat and make OpenGL think that there is more geometry to this triangle than there truly is. We will do this by passing a different normal for each vertex.
In the figure above, we define three normals of unit length (length equal to 1.0). The location of the normal is not what is important, it is the direction it points! When you work with passNormal, you're getting an interpolated value amount the normals within a primitive. This interpolation is linear which means that the passNormal is pointing in the right direction, but is usually not of unit length. That's why we renormalize each passNormal to get the true normal for that fragment as in line 5 above.
Line 6 is where we get the other vector, the light ray vector, that we will use in our calculation of the the cos𝛉. It's really important that subtract the appropriate vector from the other so you don't get the exact opposite lighting effect you intended. Here, lightPosition points from the origin to the light's position and passPosition (the interpolated position of the vertices upon the surface) points in the same direction. Generally, the passPosition is going to be shorter than the lightPosition. That means we want to subtract the passPosition from the lightPosition and not the other way around so that we end up with a vector pointing in the right direction--the same direction as the light. This vector should also be normalized before we use it in our cos𝛉 calculation.
Line 7 is where we calculate the intensity of light at that point on the surface using our cos𝛉 calculation. This value is not guaranteed to be between 0.0 and 1.0 so we use clamp() (line 8). We could also use an if statement, but I feel clamp() is more readable.
Line 9 encapsulates the lights effect. This variable will later all hold information about the ambient and specular components of light. For now it is purely affected by the diffuse component.
Line 10's surface variable definition is just a renaming of the variable that encapsulates the model's color at this fragment. It includes texture and vertex color components, but it otherwise unchanged.
Line 11 is the calculated color of the fragment once the light and surface components are combined. You could do the same within line 12, but separating it out takes less horizontal space for the blog and perhaps reads a little better as well. Regardless, line 12 is the final color of the fragment with the alpha component appended.
We have a new component that we need to add to our vertex--the normal. The new data definition layout shall be: x, y, r, g, b, s, t, nx, ny, nz.
//format: x, y, r, g, b, s, t, nx, ny, nz
[-1.0, -1.0, 1.0, 0.0, 1.0, 0.0, 2.0, -1.0, -1.0, 0.0001),
0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0001),
1.0, -1.0, 0.0, 0.0, 1.0, 2.0, 2.0, 1.0, -1.0, 0.0001)]
In the above array, I have defined the normals as pointing every so slightly in the positive z direction. Note that this makes them inherently not normalized, but since we're going to be using normalize() on each normal each time, it doesn't really matter. I made them point in the positive Z direction to give OpenGL a hint that the normal at the center of the triangle is supposed to point straight at the viewer instead of away. What we end up with is a triangle with normals like this.
The normals result an a sort of pointed surface like a cone. Even though the triangle itself is flat, these normals cause the surface to appear to have a three dimensional shape. This is the basis for bump and normal maps.
We need to add the appropriate vertex attribute as well. Our vertex is now 40 bytes and the normal attribute is, itself, 12 bytes located after the texture coordinate information (28 bytes from the address of the vertex).
glVertexAttribPointer(3, 3, GLenum(GL_FLOAT), GLboolean(GL_FALSE), 40, UnsafePointer<GLuint>
➥(bitPattern:28))
glEnableVertexAttribArray(3)
We'll also need to add the corresponding in and out attributes to the vertex shader. The position attribute will be passed to the fragment shader through the passPosition and the normal will be passed through the passNormal.
"layout (location = 3) in vec3 normal; \n"
"out vec3 passPosition; \n"
"out vec3 passNormal; \n"
We also have to add new uniforms for the light. Unlike the texture sampler uniform, these uniforms must be defined after a program is activated. We are going to define a light that casts white light and shines from the top of triangle.
glUseProgram(programID)
glUniform3fv(glGetUniformLocation(programID, "lightColor"), 1, [1.0, 1.0, 1.0])
glUniform3fv(glGetUniformLocation(programID, "lightPosition"), 1, [0.0, 1.0, 0.0])
Those are some of the highlights of the code. Below, is the full class implementation with comments.
import Cocoa
import OpenGL.GL3
final class SwiftOpenGLView: NSOpenGLView {
private var programID: GLuint = 0
private var vaoID: GLuint = 0
private var vboID: GLuint = 0
private var tboID: GLuint = 0
required init?(coder: NSCoder) {
super.init(coder: coder)
let attrs: [NSOpenGLPixelFormatAttribute] = [
UInt32(NSOpenGLPFAAccelerated),
UInt32(NSOpenGLPFAColorSize), UInt32(32),
UInt32(NSOpenGLPFAOpenGLProfile), UInt32(NSOpenGLProfileVersion3_2Core),
UInt32(0)
]
guard let pixelFormat = NSOpenGLPixelFormat(attributes: attrs) else {
Swift.print("pixelFormat could not be constructed")
return
}
self.pixelFormat = pixelFormat
guard let context = NSOpenGLContext(format: pixelFormat, shareContext: nil) else {
Swift.print("context could not be constructed")
return
}
self.openGLContext = context
}
override func prepareOpenGL() {
super.prepareOpenGL()
glClearColor(0.0, 0.0, 0.0, 1.0)
programID = glCreateProgram()
// format: x, y, r, g, b, s, t, nx, ny, nz
let data: [GLfloat] = [-1.0, -1.0, 1.0, 0.0, 1.0, 0.0, 2.0, -1.0, -1.0, 0.0001,
0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0001,
1.0, -1.0, 0.0, 0.0, 1.0, 2.0, 2.0, 1.0, -1.0, 0.0001]
let fileURL = NSBundle.mainBundle().URLForResource("Texture", withExtension: "png")
let dataProvider = CGDataProviderCreateWithURL(fileURL)
let image = CGImageCreateWithPNGDataProvider(dataProvider, nil, false,
➥.RenderingIntentDefault)
let textureData = UnsafeMutablePointer<Void>(malloc(256 * 4 * 256))
let context = CGBitmapContextCreate(textureData, 256, 256, 8, 4 * 256,
➥CGColorSpaceCreateWithName(kCGColorSpaceGenericRGB),
➥CGImageAlphaInfo.PremultipliedLast.rawValue)
CGContextDrawImage(context, CGRectMake(0.0, 0.0, 256.0, 256.0), image)
glGenTextures(1, &tboID)
glBindTexture(GLenum(GL_TEXTURE_2D), tboID)
glTexParameteri(GLenum(GL_TEXTURE_2D), GLenum(GL_TEXTURE_MIN_FILTER), GL_LINEAR)
glTexParameteri(GLenum(GL_TEXTURE_2D), GLenum(GL_TEXTURE_MAG_FILTER), GL_LINEAR)
glTexParameteri(GLenum(GL_TEXTURE_2D), GLenum(GL_TEXTURE_WRAP_S), GL_REPEAT)
glTexParameteri(GLenum(GL_TEXTURE_2D), GLenum(GL_TEXTURE_WRAP_T), GL_REPEAT)
glTexImage2D(GLenum(GL_TEXTURE_2D), 0, GL_RGBA, 256, 256, 0, GLenum(GL_RGBA),
➥GLenum(GL_UNSIGNED_BYTE), textureData)
free(textureData)
glGenBuffers(1, &vboID)
glBindBuffer(GLenum(GL_ARRAY_BUFFER), vboID)
glBufferData(GLenum(GL_ARRAY_BUFFER), data.count * sizeof(GLfloat), data,
➥GLenum(GL_STATIC_DRAW))
glGenVertexArrays(1, &vaoID)
glBindVertexArray(vaoID)
glVertexAttribPointer(0, 2, GLenum(GL_FLOAT), GLboolean(GL_FALSE), 40,
➥UnsafePointer<GLuint>(bitPattern: 0))
glEnableVertexAttribArray(0)
glVertexAttribPointer(1, 3, GLenum(GL_FLOAT), GLboolean(GL_FALSE), 40,
➥UnsafePointer<GLuint>(bitPattern: 8))
glEnableVertexAttribArray(1)
glVertexAttribPointer(2, 2, GLenum(GL_FLOAT), GLboolean(GL_FALSE), 40,
➥UnsafePointer<GLuint>(bitPattern: 20))
glEnableVertexAttribArray(2)
// The fourth attribute, the normal. This adds an addition 12 bytes to the vertex
// The vertex's total byte count is now 40 and the normal may be found at the end
// of the previous attribute, byte 28
glVertexAttribPointer(3, 3, GLenum(GL_FLOAT), GLboolean(GL_FALSE), 40,
➥UnsafePointer<GLuint>(bitPattern:28))
glEnableVertexAttribArray(3)
glBindVertexArray(0)
// The fragment shader is going to need the vertex position and normal, so we pass
// those values on. The vertex shader remains otherwise unchanged.
let vs = glCreateShader(GLenum(GL_VERTEX_SHADER))
var source = "#version 330 core \n" +
"layout (location = 0) in vec2 position; \n" +
"layout (location = 1) in vec3 color; \n" +
"layout (location = 2) in vec2 texturePosition; \n" +
"layout (location = 3) in vec3 normal; \n" +
"out vec3 passPosition; \n" +
"out vec3 passColor; \n" +
"out vec2 passTexturePosition; \n" +
"out vec3 passNormal; \n" +
"void main() \n" +
"{ \n" +
" gl_Position = vec4(position, 0.0, 1.0); \n" +
" passPosition = vec3(position, 0.0); \n" +
" passColor = color; \n" +
" passTexturePosition = texturePosition; \n" +
" passNormal = normal; \n" +
"} \n"
if let vss = source.cStringUsingEncoding(NSASCIIStringEncoding) {
var vssptr = UnsafePointer<GLchar>(vss)
glShaderSource(vs, 1, &vssptr, nil)
glCompileShader(vs)
var compiled: GLint = 0
glGetShaderiv(vs, GLbitfield(GL_COMPILE_STATUS), &compiled)
if compiled <= 0 {
Swift.print("Could not compile vertex, getting log")
var logLength: GLint = 0
glGetShaderiv(vs, GLenum(GL_INFO_LOG_LENGTH), &logLength)
Swift.print(" logLength = \(logLength)")
if logLength > 0 {
let cLog = UnsafeMutablePointer<CChar>(malloc(Int(logLength)))
glGetShaderInfoLog(vs, GLsizei(logLength), &logLength, cLog)
if let log = String(CString: cLog, encoding: NSASCIIStringEncoding) {
Swift.print("log = \(log)")
free(cLog)
}
}
}
}
// Here is where the bulk of the changes take place and where the actual computing
// change takes place.
// The light source is defined by a color and a position that are the same for every
// fragment. Therefore, we pass them in as uniform variables.
// The normal must be renormalized as it is an interpolated value when passed from the
// vertex shader.
// The light ray incident to this fragment is calculated from the interpolated position
// and the light position. This vector should also be normalized to simplify our
// calculations--as we shall see in a moment.
// The intensity of light upon the fragment, is calculated using the dot product and it's
// equivalent equation |A||B|cos𝛉. Solving for cos𝛉, we get the euqation
// dot(A, B) / length(A) * length(B)
// Because we normalized the normal and the light ray vectors, we can simplify this to
// dot(A, B)
// This value is clamped to a value between 0 and 1 because the calculation may return a
// a negative value.
// The light variable is simple now, but will become complete later. For now it is a
// simple pass on.
// The model color is calculated the same as before.
// Then the final color of the fragment is calculated by combining the light and surface
// colors and added on the alpha value.
let fs = glCreateShader(GLenum(GL_FRAGMENT_SHADER))
source = "#version 330 core \n" +
"uniform sampler2D sample; \n" +
"uniform vec3 lightColor; \n" +
"uniform vec3 lightPosition; \n" +
"in vec3 passPosition; \n" +
"in vec3 passColor; \n" +
"in vec2 passTexturePosition; \n" +
"in vec3 passNormal; \n" +
"out vec4 outColor; \n" +
"void main() \n" +
"{ \n" +
" vec3 normal = normalize(passNormal); \n" +
" vec3 lightRay = normalize(lightPosition - passPosition); \n" +
" float intensity = dot(normal, lightRay); \n" +
" intensity = clamp(intensity, 0, 1); \n" +
" vec3 light = lightColor * intensity; \n" +
" vec3 surface = texture(sample, passTexturePosition).rgb * passColor; \n" +
" vec3 rgb = surface * light; \n" +
" outColor = vec4(rgb, 1.0); \n" +
"} \n"
if let fss = source.cStringUsingEncoding(NSASCIIStringEncoding) {
var fssptr = UnsafePointer<GLchar>(fss)
glShaderSource(fs, 1, &fssptr, nil)
glCompileShader(fs)
var compiled: GLint = 0
glGetShaderiv(fs, GLbitfield(GL_COMPILE_STATUS), &compiled)
if compiled <= 0 {
Swift.print("Could not compile fragement, getting log")
var logLength: GLint = 0
glGetShaderiv(fs, GLbitfield(GL_INFO_LOG_LENGTH), &logLength)
Swift.print(" logLength = \(logLength)")
if logLength > 0 {
let cLog = UnsafeMutablePointer<CChar>(malloc(Int(logLength)))
glGetShaderInfoLog(fs, GLsizei(logLength), &logLength, cLog)
if let log = String(CString: cLog, encoding: NSASCIIStringEncoding) {
Swift.print("log = \(log)")
free(cLog)
}
}
}
}
glAttachShader(programID, vs)
glAttachShader(programID, fs)
glLinkProgram(programID)
var linked: GLint = 0
glGetProgramiv(programID, UInt32(GL_LINK_STATUS), &linked)
if linked <= 0 {
Swift.print("Could not link, getting log")
var logLength: GLint = 0
glGetProgramiv(programID, UInt32(GL_INFO_LOG_LENGTH), &logLength)
Swift.print(" logLength = \(logLength)")
if logLength > 0 {
let cLog = UnsafeMutablePointer<CChar>(malloc(Int(logLength)))
glGetProgramInfoLog(programID, GLsizei(logLength), &logLength, cLog)
if let log = String(CString: cLog, encoding: NSASCIIStringEncoding) {
Swift.print("log: \(log)")
}
free(cLog)
}
}
glDeleteShader(vs)
glDeleteShader(fs)
let sampleLocation = glGetUniformLocation(programID, "sample")
glUniform1i(sampleLocation, GL_TEXTURE0)
// Before we define our light's attributes, we need to select a program
glUseProgram(programID)
// Define the parameters for a light.
// We'll start our light definition with a color and a position.
// The color and position contain three components -- use a 3fv uniform
// 3 for three components, f for float, v for variable
// Alternatively, you could use a uniform3f which allows you to send three floats as
// separate parameters
glUniform3fv(glGetUniformLocation(programID, "lightColor"), 1, [1.0, 1.0, 1.0])
glUniform3fv(glGetUniformLocation(programID, "lightPosition"), 1, [0.0, 1.0, 0.0])
drawView()
}
override func drawRect(dirtyRect: NSRect) {
super.drawRect(dirtyRect)
// Drawing code here.
drawView()
}
private func drawView() {
glClear(GLbitfield(GL_COLOR_BUFFER_BIT))
glUseProgram(programID)
glBindVertexArray(vaoID)
glDrawArrays(GLenum(GL_TRIANGLES), 0, 3)
glBindVertexArray(0)
glFlush()
}
deinit {
glDeleteVertexArrays(1, &vaoID)
glDeleteBuffers(1, &vboID)
glDeleteProgram(programID)
glDeleteTextures(1, &tboID)
}
}
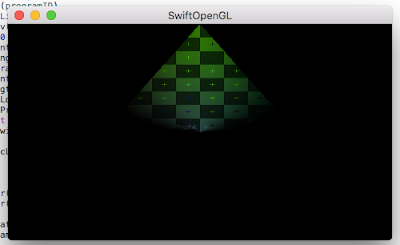
Run the program, and you'll see a partially lit triangle.
This post had a lot of "ground work" to discuss with only a few changes in the class overall. However, when you run the program, you can see the major effect it has had on the triangle. Notice that cone shop we discussed earlier? You only see the top of the triangle because our triangle's normals are telling OpenGL that the two bottom corners are pointing away from the light and are thus in shadow.
Next time, we'll add the last two components of our lighting model: ambient and specular. A lighting model calculated in the fragment shader using ambient, diffuse (what we have done here), and specular is known as the Phong shading model. In contrast, lighting done in the vertex shader is called Gouraud shading. For now, try moving the light around, and playing with the lighting calculations to see the different effect each calculation has on the lighting.
Please comment and help me make these tutorials better! If there was anything confusing, or could have been explained better or more succinctly, let me know in the comments! Thank you following this far!
When you're ready, let's add ambient and specular.
You can find the project target, LitTriangle, on GitHub.
Next time, we'll add the last two components of our lighting model: ambient and specular. A lighting model calculated in the fragment shader using ambient, diffuse (what we have done here), and specular is known as the Phong shading model. In contrast, lighting done in the vertex shader is called Gouraud shading. For now, try moving the light around, and playing with the lighting calculations to see the different effect each calculation has on the lighting.
Please comment and help me make these tutorials better! If there was anything confusing, or could have been explained better or more succinctly, let me know in the comments! Thank you following this far!
When you're ready, let's add ambient and specular.
You can find the project target, LitTriangle, on GitHub.








Comments
Post a Comment